Expert Heads Up No Limit Hold’em: Excerpt 1
This is the first excerpt from Will Tipton’s book Expert Heads Up No Limit Hold’em Vol 1: Optimal and Exploitative Strategies. The book is on sale at www.dandbpoker.com from 14th of December 2012.
Excerpt 1
It is often said that the game of heads-up no-limit hold ’em is too large and complicated to be solved with modern computers. However, it might not be clear precisely what is meant by this. What exactly is the entire game of HUNL? How would we write it down? What would it mean to solve it? If we had such a solution, how could we use it to play better poker, anyway? And what strategic progress might be made without the full solution?
We can describe the entire game of HUNL most elegantly by writing it down in the form of a decision tree. This tree is often drawn as a set of points connected by lines. Each point, called a decision point, represents a spot where one of the players must make a decision to take one or more actions. Each possible action is represented by a line coming off from the point. point. We may also refer to the set of actions available to a player as choices, options, or strategic options.
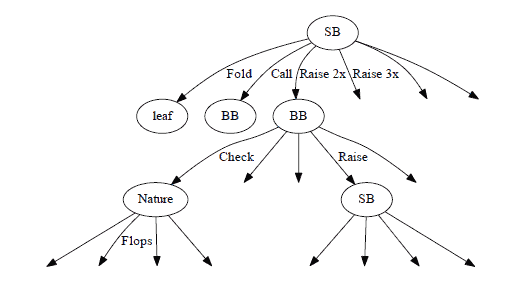
Figure 1.1 is an example of a section of a decision tree. The tree begins at a decision point known as the root which we will generally draw at the top. In HUNL games, the root decision point is controlled by the SB, and in this example, he has the option to fold or raise. If he chooses to raise, the play moves down the line labelled “raise” to a decision point controlled by the BB who then has several actions available to him. To fully specify the game, it is also necessary to give the players’ stack sizes at the beginning of the hand.
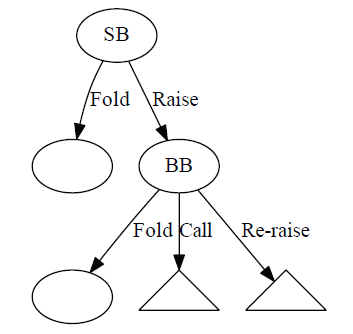
Figure 1.1: Example portion of a decision
tree. Triangles are used to indicate that
the whole tree continues but is not shown.
This tree segment can be thought of as the beginning of a HUNL hand. After the blinds are posted, the SB acts first, and unless he folds, the BB acts next. Of course, this is a simplified version of a game since, in the full game, the SB has more than two actions open to him at the beginning of the hand. In addition to folding, he may also call or raise to one of many different sizes. Each of these many choices would lead to a different BB decision point.
The BB, similarly, has many choices in the full game. The BB may choose to fold, in which case the hand is over. He may re-raise, and again each possible re-raise sizing leads to a distinct SB decision point. Additionally, the BB may choose to call. In this case, the game moves to a special type of decision point which is controlled by neither the SB nor the BB. It is generally said to be controlled by God or Nature, and the choice being made is that of which flop to deal. Nature will have similar decisions to make when it comes time to deal the turn and river cards.
Figure 1.2 shows an expanded decision tree which indicates that many raise sizes are possible and that Nature decides which cards to deal at the appropriate points. It also shows a few points which lead to no further action. For example, suppose the SB starts the hand by immediately folding. The hand is over, and we arrive at the point labeled “leaf” on the figure. Since this point is the end of a path through the tree and is furthest from the root, it is known as a leaf. (Clever, eh?) In general, these are the decision points reached by the a fold, a call of an all-in bet, or a hand-ending action at the end of river play. Since leaves represent the end of a hand, they are where payoffs happen.
A complete path from the root to a leaf may be called a line. This is essentially the same as the use of the word line in colloquial poker-speak. It refers to one complete set of actions that both players can take given particular community cards. Additionally, if you start at any particular decision point, call it A, then it, along with any decisions and actions which can be reached by moving down the tree are known as the subtree or subgame beginning at A. The two subtrees reached after the SB raises and the BB calls or re-raises are indicated by triangles in Figure 1.1. The depth of the tree is the greatest number of actions between the root and any of its leaves.
Now, we have still not shown the decision tree for the full game. Many raise/reraise/ re-raise possibilities have been neglected, not to mention all the possible flops, turns, and rivers. This is in the interest of space. Keep in mind that every possible different combination of preflop actions leads to a whole different flop subtree and for each of these, many different flop plays are possible, each of which leads to distinct turn and river subtrees. We will turn to an approximation of the size of the full tree shortly, but first, we consider strategies for playing the games described by a tree.
Now that we know how to describe a game by organizing all of the different situations which may arise into a tree format, how do we describe strategies for playing that game?
Very simply, a player’s strategy must describe what he will do in any situation he can face in the game. That is, it specifies how he will play each hand in his range at each of his decision points. In practice, this means that to describe a player’s strategy, every action which he can take must have a range associated with it which specifies the hands with which he takes that action. Furthermore, at any particular decision point, all of the actions he can take must have ranges that “add up” to the range of hands with which he got to that decision point in the first place.